The
butterfly effect is a metaphor that encapsulates the concept of
sensitive dependence on initial conditions in
chaos theory; namely a small change at one place in a complex system can have large effects elsewhere. Although this may appear to be an esoteric and unusual behavior, it is exhibited by very simple systems: for example, a
ball placed at the crest of a hill might roll into any of several valleys depending on slight differences in initial position. The butterfly effect is a common
trope in fiction when presenting scenarios involving
time travel and with "what if" cases where one storyline diverges at the moment of a seemingly minor event resulting in two significantly different outcomes.
Recurrence, the approximate return of a system towards its initial conditions, together with sensitive dependence on initial conditions are the two main ingredients for chaotic motion. They have the practical consequence of making
complex systems, such as the
weather, difficult to predict past a certain time range (approximately a week in the case of weather), since it is impossible to measure the starting atmospheric conditions completely accurately.
[edit]Origin of the concept and the term
The term "butterfly effect" itself is related to the work of
Edward Lorenz, and is based in
chaos theory and sensitive dependence on initial conditions, already described in the literature in a particular case of the
three-body problem by
Henri Poincaré in 1890.
[1] He later proposed that such phenomena could be common, say in meteorology. In 1898
[1] Jacques Hadamard noted general divergence of trajectories in spaces of negative curvature, and
Pierre Duhem discussed the possible general significance of this in 1908.
[1] The idea that one
butterflycould eventually have a far-reaching
ripple effect on subsequent historic events seems first to have appeared in
A Sound of Thunder, a 1952 short story by
Ray Bradbury about time travel (
see Literature and print here) although Lorenz made the term popular. In 1961, Lorenz was using a numerical computer model to rerun a weather prediction, when, as a shortcut on a number in the sequence, he entered the decimal .506 instead of entering the full .506127 the computer would hold. The result was a completely different weather scenario.
[2] Lorenz published his findings in a 1963 paper
[3] for the
New York Academy of Sciences noting
[citation needed] that "One meteorologist remarked that if the theory were correct, one flap of a
seagull's wings could change the course of weather forever." Later speeches and papers by Lorenz used the more poetic
butterfly. According to Lorenz, upon failing to provide a title for a talk he was to present at the 139th meeting of the
American Association for the Advancement of Science in 1972, Philip Merilees concocted
Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas? as a title. Although a butterfly flapping its wings has remained constant in the expression of this concept, the location of the butterfly, the consequences, and the location of the consequences have varied widely.
[4]The phrase refers to the idea that a
butterfly's wings might create tiny changes in the
atmosphere that may ultimately alter the path of a
tornado or delay, accelerate or even prevent the occurrence of a tornado in a certain location. The flapping wing represents a small change in the initial condition of the system, which causes a chain of events leading to large-scale alterations of events (compare:
domino effect). Had the butterfly not flapped its wings, the trajectory of the system might have been vastly different. While the butterfly does not "cause" the tornado in the sense of providing the energy for the tornado, it does "cause" it in the sense that the flap of its wings is an essential part of the initial conditions resulting in a tornado, and without that flap that particular tornado would not have existed.
llustration
| The butterfly effect in the Lorenz attractor |
|---|
| time 0 ≤ t ≤ 30 (larger) | z coordinate (larger) |
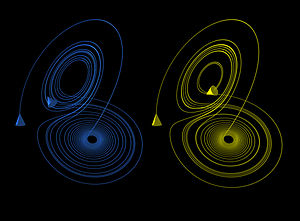 | 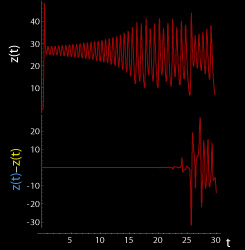 |
| These figures show two segments of the three-dimensional evolution of two trajectories (one in blue, the other in yellow) for the same period of time in the Lorenz attractor starting at two initial points that differ only by 10−5 in the x-coordinate. Initially, the two trajectories seem coincident, as indicated by the small difference between the z coordinate of the blue and yellow trajectories, but for t > 23 the difference is as large as the value of the trajectory. The final position of the cones indicates that the two trajectories are no longer coincident at t=30. |
| A Java animation of the Lorenz attractor shows the continuous evolution. |
[edit]Mathematical definition
A
dynamical system with evolution map
ft displays sensitive dependence on initial conditions if points arbitrarily close together become separate with increasing
t at an exponential rate. The definition is not topological, but essentially metrical.
If M is the state space for the map ft, then ft displays sensitive dependence to initial conditions if for any x in M and any δ>0, there are y inM, with 0 < d(x,y) < δ such that.
- d(fτ(x),fτ(y)) > exp(aτ)d(x,y).
The definition does not require that all points from a neighborhood separate from the base point
x, but it requires one positive
Lyapunov exponent.
[edit]Examples in semiclassical and quantum physics
The potential for sensitive dependence on initial conditions (the butterfly effect) has been studied in a number of cases in
semiclassical and
quantum physics including atoms in strong fields and the anisotropic
Kepler problem.
[5][6] Some authors have argued that extreme (exponential) dependence on initial conditions is not expected in pure quantum treatments;
[7][8] however, the sensitive dependence on initial conditions demonstrated in classical motion is included in the semiclassical treatments developed by
Martin Gutzwiller[9] and Delos and co-workers.
[10]Other authors suggest that the butterfly effect can be observed in quantum systems. Karkuszewski et al. consider the time evolution of quantum systems which have slightly different Hamiltonians. They investigate the level of sensitivity of quantum systems to small changes in their given Hamiltonians.
[11] Poulin et al. present a quantum algorithm to measure fidelity decay, which “measures the rate at which identical initial states diverge when subjected to slightly different dynamics.” They consider fidelity decay to be “the closest quantum analog to the (purely classical) butterfly effect.”
[12] Whereas the classical butterfly effect considers the effect of a small change in the position and/or velocity of an object in a given
Hamiltonian system, the quantum butterfly effect considers the effect of a small change in the
Hamiltonian system with a given initial position and velocity.
[13][14] This quantum butterfly effect has been demonstrated experimentally.
[15] Quantum and semiclassical treatments of system sensitivity to initial conditions are known as
quantum chaos.
[7][13][edit]Preceding ideas
In 1893,
Nikola Tesla noted: "A single ray of light from a distant star falling upon the eye of a tyrant in bygone times may have altered the course of his life, may have changed the destiny of nations, may have transformed the surface of the globe, so intricate, so inconceivably complex are the processes in Nature."
[16]

